
|
(From "Outer dynamics and escapes in barred galaxies" Contopoulos and Patsis 2006, MNRAS in press) |
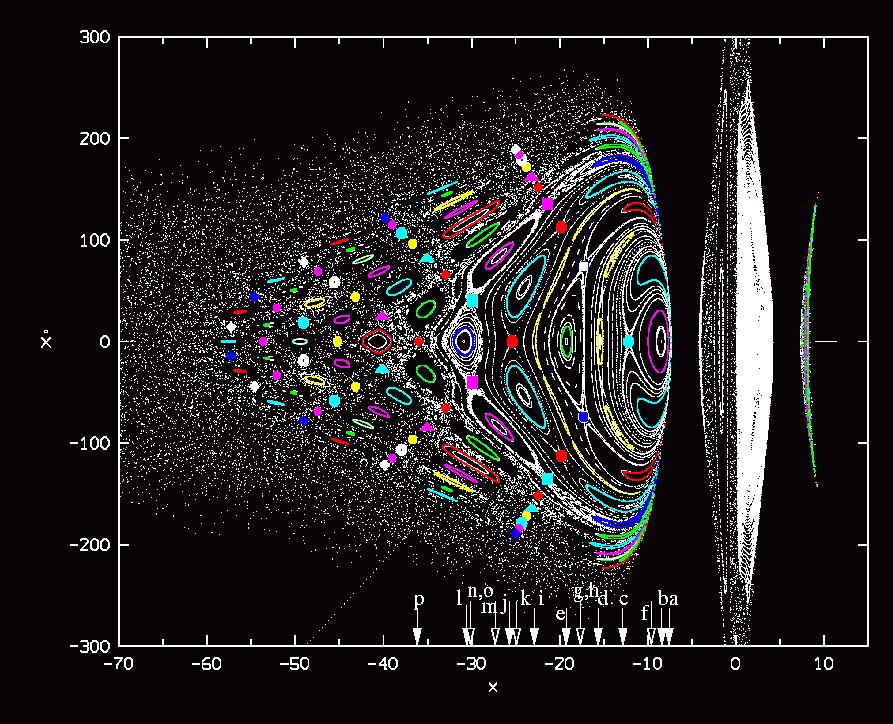
We study the dynamics of the outer parts of barred galaxies (beyond corotation). In this region there are several islands of stability around stable periodic orbits and chaotic orbits that eventually escape from the galaxy. We study the forms of the orbits (periodic and nonperiodic) and the intersections of the orbits by a surface of section $(x,\dot{x})$, i.e. $y=0$, for fixed values of the Jacobi constant. The structure of phase space is characterized by the {\em rotation curve}, i.e. the rotation number of successive orbits with initial conditions along the x-axis. The nonescaping orbits have initial conditions inside a ``last KAM torus''. The escaping orbits either have a positive energy from the beginning, or they change their energy at irregular intervals of time, acquiring finally positive energy that leads to escape. The successive consequents (intersections) of such an orbit are along ``bell-type curves'' (one curve for each value of the energy). On the surface of section we see also almost rectilinear ``rays'' that are the images of the x-axis (i.e. $\dot{x}=y=0$). The lower parts of these rays represent escaping orbits. These escapes are much faster than the escapes produced by encounters of stars among themselves. We considered two models of galactic type and various values of the Jacobi constant. These models have the same basic behaviour as regards the nonescaping and escaping orbits. This is an indication that these phenomena are characteristic of the outer parts of generic rotating galaxies. The Figure shows the net of islands that prevents orbits
from escaping. Colors are used in order to distinguish islands of stability
or hyperbolic points belonging to the same orbit (see text). From Patsis 2005, MNRAS 358,305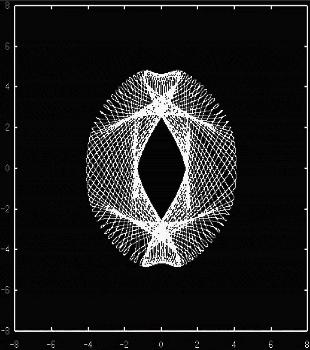
From Kaufmann and Patsis 2005, ApJ 624,693 Kaufmann and Patsis (2005) presented evidence that in two-dimensional
models with sufficiently large bar axial ratios (a/c>~6), stable
orbits having propeller shapes play the dominant role. In our models
this propeller family is in fact a distant relative of the x1
family. There are also intermediate cases in which both families are
important. The dominance of one family over the other may have direct
consequences on the morphological properties of the bars that can be
constructed from them, properties such as face-on bar thinness and
strength as well as the boxiness of the outer isophotes.
(From Boonyasait, Patsis and Gottesman, 2005)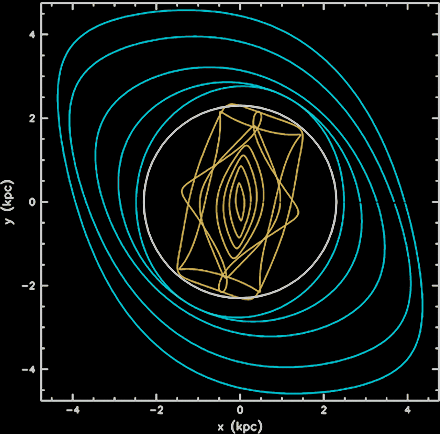
This is the best theoretical representation for the (inner 5 kpc) morphology of the galaxy NGC 3359. It combines x1 orbits from two models rotating with two different pattern speeds. The white circle denotes the extent of the stellar bar. Orbits with the same color belong to the same model. (From Patsis, Athanassoula, Quillen 1997, ApJ 483,717)In a paper by Patsis, Athanassoula and Quillen (1997) we found the main families of simple periodic orbits in and around the bar of NGC 4314 and examined their stability. We have given special attention to the orbital behavior at the ultraharmonic resonance region, and we investigated all possibilities offered by our study in explaining the boxy structure at the end of the bar. It has been shown that the outer boxy isophotes in this and other early type bars, are in a large extent due to the chaotic orbits at the region. The contribution of chaotic orbits to the boxiness of the bar is described at the figure above. It shows three chaotic orbits, integrated for a few pattern rotations, suppoorting a boxy structure. References:
|