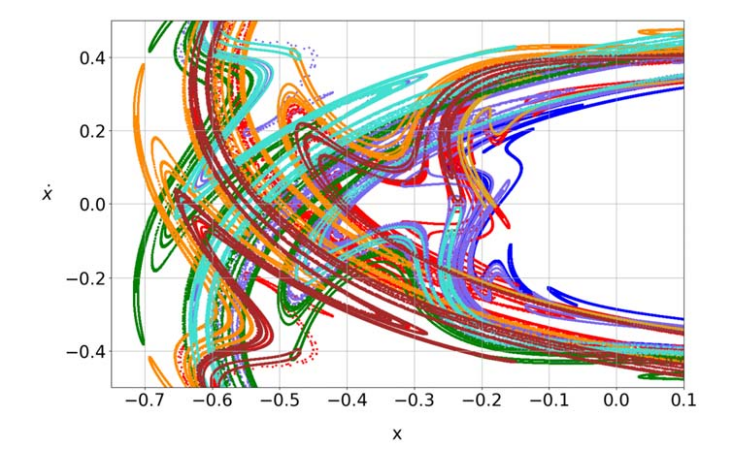
Resonance overlap is a fundamental mechanism for the onset of chaos in near-integrable Hamiltonian systems. As nonlinear resonances widen with increasing perturbation strength, they begin to intersect, leading to the destruction of invariant tori that normally partition phase space. Once these barriers are removed, trajectories can move between resonant regions, giving rise to extended chaotic motion and large-scale phase-space transport. This figure illustrates this mechanism through a Poincaré surface of section of a generalized Hénon–Heiles Hamiltonian in the resonance-overlap regime. The curves shown are the stable and unstable asymptotic manifolds associated with different unstable periodic orbits. Their transverse intersections generate a dense network of homoclinic and heteroclinic tangles, providing the geometric framework that organizes chaotic dynamics and transport across the phase space.

References:

1) Contopoulos, G., Tzemos, A. C., & Zanias, F. (2025). Integrals and chaos in generalized Hénon–Heiles Hamiltonians. Physica Scripta, 100, 045225

2) Tzemos, A. C., Contopoulos, G., & Zanias, F. (2025). Orbits in the integrable Hénon–Heiles systems. Physica Scripta, 100, 055233