Pictures archive
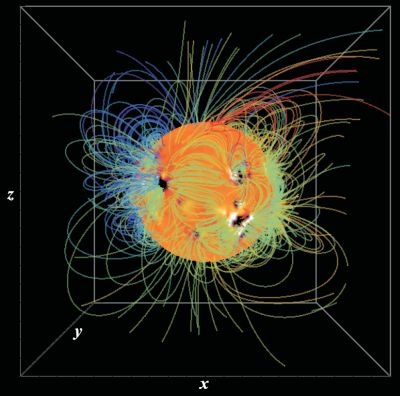
Inner pulsar magnetosphere

The pulsar magnetosphere near the stellar surface as obtained with Physics Informed Neural Networks (PINNs). Magnetic axis inclined by 20 degrees with respect to the vertical rotation axis. Orange lines: open magnetic field lines from the north and south polar caps (delineated by the magenta circles). Blue lines: closed field lines. Transparent magenta lines: dipolar field lines that would have originated from the same points in the north stellar hemisphere. We observe an interesting twist of closed field lines due to the fast stellar rotation (see Dimitropoulos & Contopoulos 2024 for details; arXiv: 2410.10716).
Relativistic magnetohydrodynamics simulation
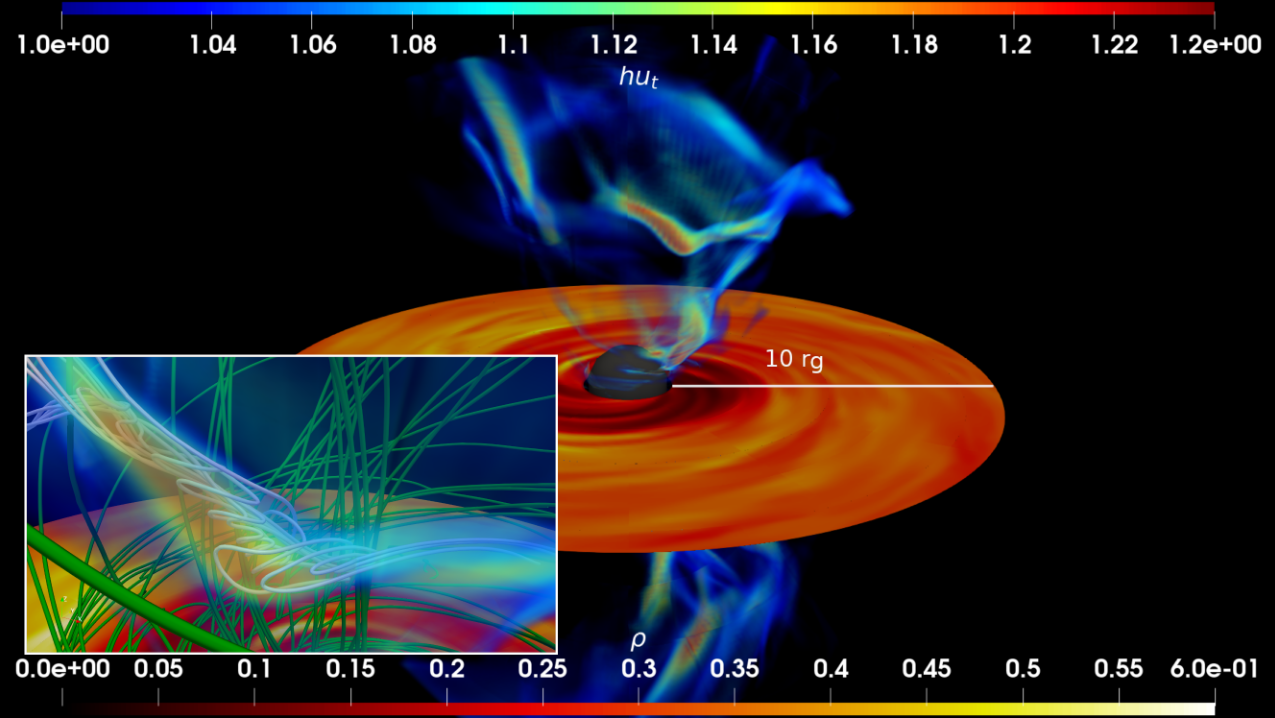
Three-dimensional view of the magnetization (σ) from a general relativistic magnetohydrodynamics simulation. The rest-mass density is depicted exclusively on the equatorial plane to visualize the disk's rotation (with a disc radius of 30 rg). The magnetization color code ranges from 1.00 to 1.20, highlighting highly magnetized regions with σ > 1.15 as plasmoids. Inset: A close-up view of the largest plasmoid within the snapshot; magnetic fields outside the plasmoid are shown in green, while those inside are cyan. Magnetic field lines inside the plasmoid are tangled and are expected to have a distribution of high energy particles radiating and observed as a black hole flare. Plasmoids, magnetic structures of various sizes and lifetimes, play pivotal roles in our study. We have identified three distinct launching sites for these plasmoids: the low-density funnel, the turbulent interior of the disk, and the jet sheath. Each site yields plasmoids with unique characteristics and dynamics. Here, we observe at least two plasmoids, each exhibiting a non-spherical, filamentous morphology, influenced by the shearing motion in the background flow. Smaller plasmoids are frequently generated but either accrete onto the black hole or are swiftly destroyed by shear forces. In contrast, larger plasmoids, surviving for longer duration, are rare occurrences. Our simulations reveal that no plasmoids persist beyond a spherical region approximately 30 rg from the black hole's event horizon. Beyond this boundary, all plasmoids transform into high-temperature clouds, gradually cooling over time. This comprehensive analysis offers valuable insights into the complex dynamics and fates of plasmoids in our simulated environment, contributing to a deeper understanding of astrophysical phenomena.
Reference: Nathanail, A., Mpisketzis, V., Porth, O., Fromm, C. M. Rezzolla, L. Magnetic reconnection and plasmoid formation in three-dimensional accretion flows around black holes,Monthly Notices of the Royal Astronomical Society, Volume 513, Issue 3, pp.4267-4277 July 2022
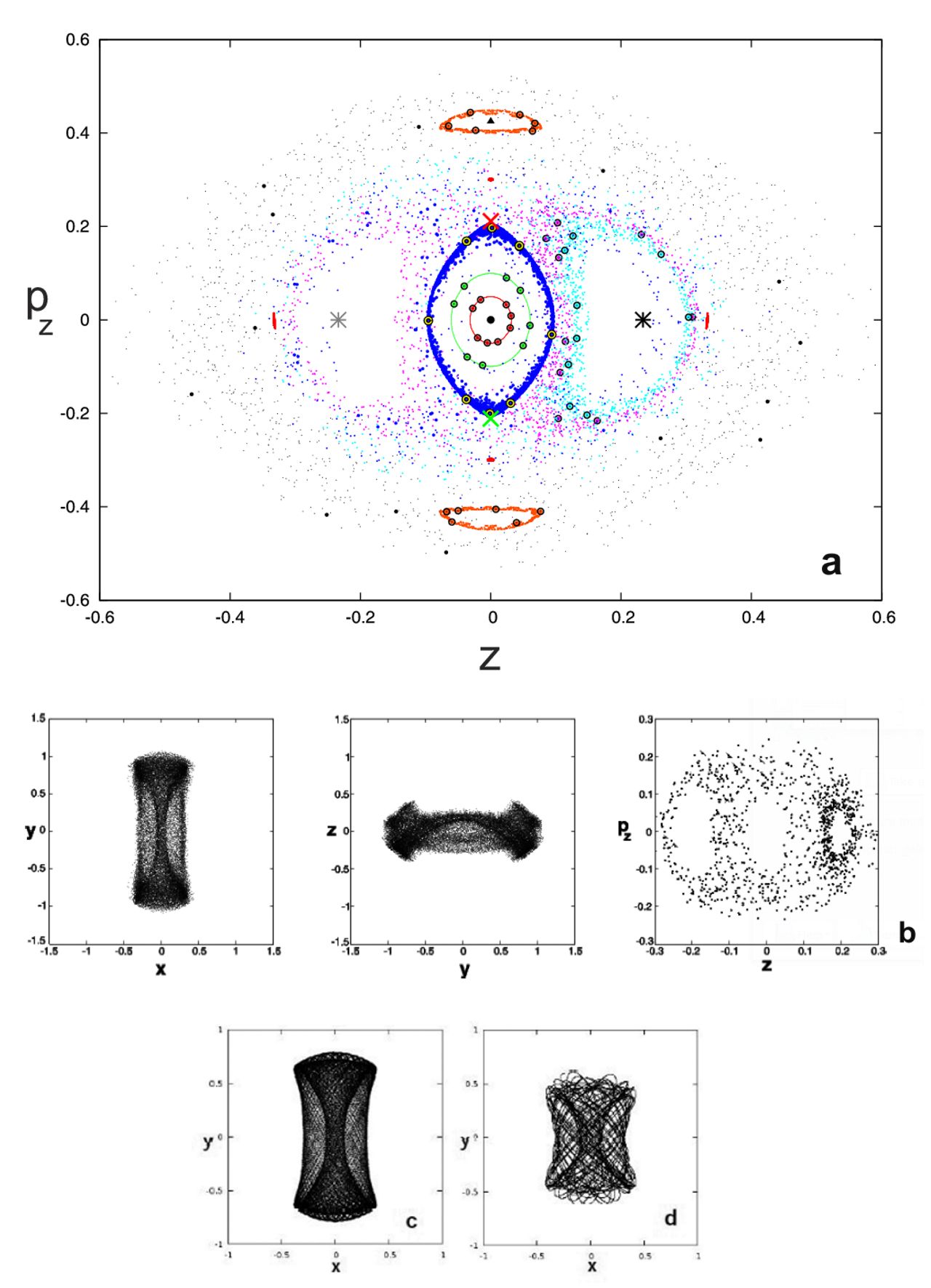
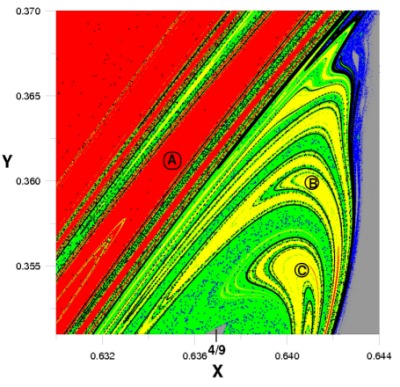
Phase Space Structure in the vicinity of vertical Lyapunov orbits around L1,2 in a barred galaxy model
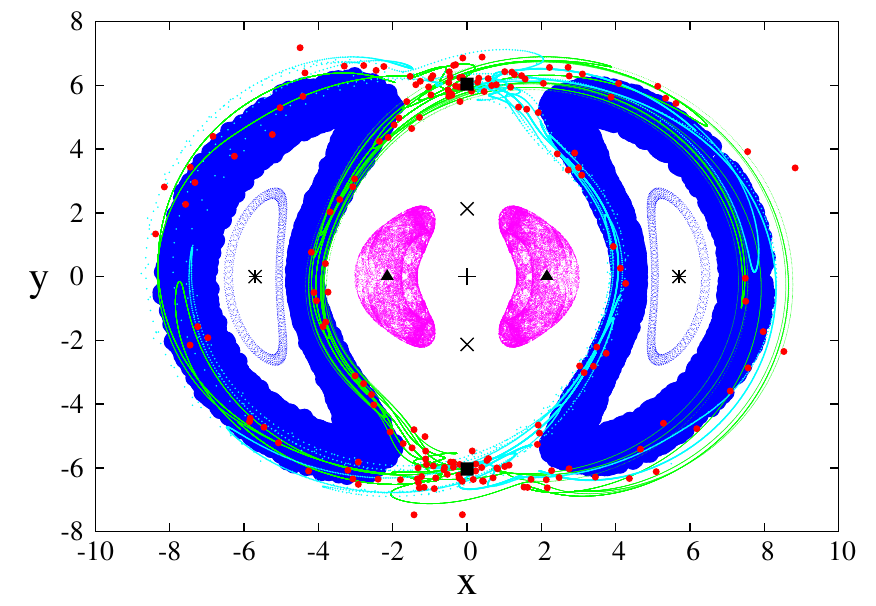
The picture shows the phase space structure and the orbital diffusion from the vicinity of the vertical Lyapunov periodic orbits (vLPOs) around the unstable Lagrangian points L1,2 in a 3D barred galaxy model. In particular, we see the (x,y) projection of the (x,y,p_x,p_y) 4D space of section (we consider the Poincare section z=0 with pz>0), for the consequents and invariant manifolds associated with the diffusion of 3D orbits that form the neighborhood of vLPOs around L1 and L2 for a value of energy E=-0.165. The initial conditions of the two vLPOs are indicated with black squares, while those of the vertical POs around L4,5 with black stars. Furthermore, the central cross corresponds to the initial conditions of the POs of the z-axis family (coincides with the location of L3), black triangles mark the location of the two sao POs (stable anomalous orbits - initially stable bifurcations of the z-axis family) and the X symbols those of the two uao ones (unstable anomalous orbits - initially unstable bifurcations of the z-axis family). The 190 consequents of the double-crescent orbit (that is formed in the neighborhood of the vLPOs of L1,2 - see Katsanikas and Patsis 2022) are given with heavy red dots. The 2D projection of the unstable invariant manifolds of the simple unstable vLPOs around L1 and L2 are drawn with green and cyan colors respectively. We see that the projections of the tori around the stable L4,5 are drawn with blue, while those around the sao POs with magenta color. We observe that the points forming the double-crescent are sticky on the unstable invariant manifolds of the simple unstable POs around the Lagrangian points L1,2. The manifolds are guided from the invariant tori that are found around the stable vertical periodic orbits associated with the Lagrangian points L4,5. This landscape offers an illustrative representation of the main structures existing in the phase space we study.
References:
1) M.Katsanikas and P.Patsis, The Phase Space Structure in the vicinity of
vertical Lyapunov orbits around L1,2 in a barred galaxy model, MNRAS, 516,
5232-5243 (2022).
Gaflows in barred galaxies with big orbital loops
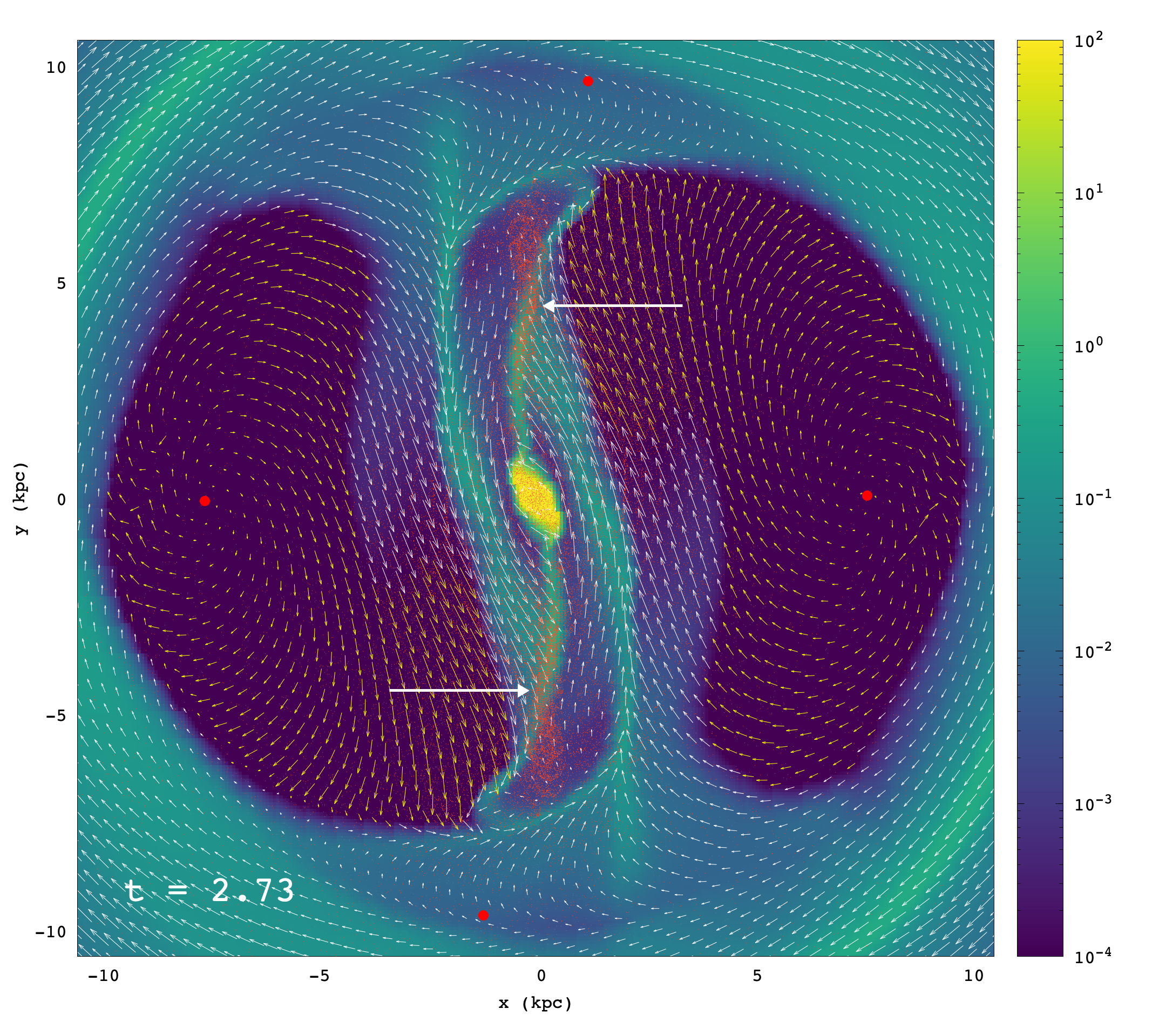
The gas response in a barred galaxy model, in which the orbital backbone of the bar, i.e. the orbits of the x1 family, have big loops close to the end of the bar, shows sevaral interesting features. In a recent study (Pastras, Patsis, Athanassoula 2022) we found that he dust-lane shocks in the gas responses of barred galaxies models avoid the regions in which the stable POs of the x1 family have developed sufficiently big loops. They deviate from these regions and, as they bypass them, they form extensions at an angle with the straight-line shocks. Ahead of them, in the direction of rotation, we find low-density regions, which in many cases have a “triangular”-like shape. We reach this conclusion by means of two conceptually different hydrodynamic schemes for our calculations, namely, the mesh-free Lagrangian SPH method and the adaptive mesh refinement code RAMSES. This allows us to compare responses by means of the two algorithms.
In the frame above, we present a typical snapshot of our RAMSES simulation, summarizing the main morphological features, together with the velocity vectors indicating the flow. The flow vectors are colored yellow, when they are in regions below the minimum density we considered. The two long white arrows indicate the point where the tails of the Γ features join the dust-lane shocks in the bar region. The stellar response is given in the background using a red color for the test particles. Red dots give the locations of the Lagrangian points.
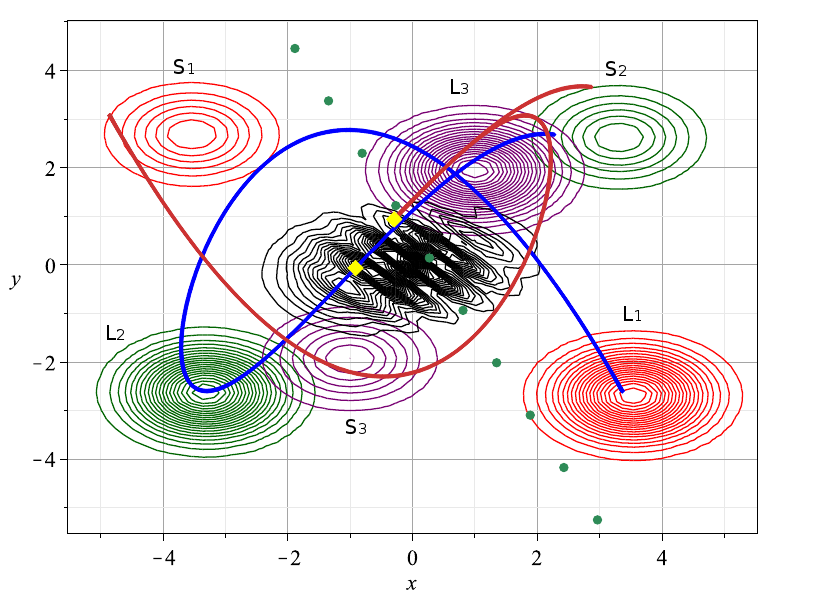
The picture shows a typical collision event between the blobs of the wavefunction describing two entangled qubits and the segments of two Bohmian trajectories, one ordered (blue) and one chaotic (red). The blue trajectory starts on the leading blob (L1) and the chaotic trajectory on the small blob (S1). Both of them follow the motion of these blobs (L2, S2) up to the collision event (black contours). Then the ordered trajectory retains its placement on the leading blob (L3), while the chaotic trajectory exhibits an abrupt change in its direction and follows the leading blob (L3) instead of the small blob (S3). This happens due to the interaction of the chaotic trajectory with a NPXPC, during the collision, when this trajectory is at the yellow square (green dots represent the nodal points at the collision time t = 4,5). The ordered trajectory does not undergo such a scattering and continues following the large blob. In the case of chaotic trajectories, this mechanism leads an arbitrary distribution of initial conditions to the distribution which satisfies Born’s rule.
References:
- Efthymiopoulos, C., Kalapotharakos, C., and Contopoulos, G.: 2009, Phys. Rev. E 79, 036203
- Tzemos, A.C, Contopoulos, G., and Efthymiopoulos, C.:2019, Phys. Scr. 94 (2019) 105218
- Tzemos, A.C, Contopoulos, G.: 2020 arXiv:2003.03989
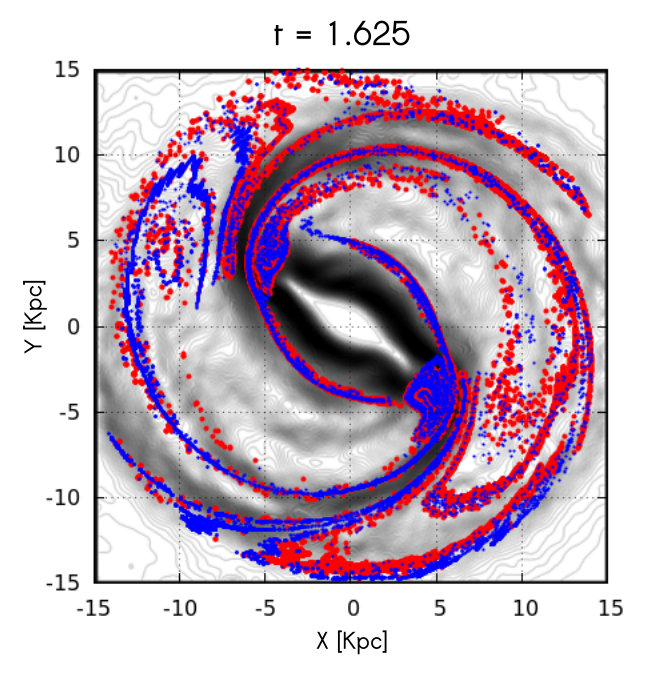
The picture shows the applicability of the manifold theory of spiral arms in N-body simulations of barred-spiral galaxies. The red and blue points visualize the `apocentric' unstable manifolds emanating from periodic orbits in the neighborhood of the bar's Lagrangian points L1 and L2. These manifolds support `chaotic spirals' (Patsis 2006) in the form of outflows from the region of L1 or L2. The dark contour lines produce the image of the disc in the N-body simulation using the Sobel-Feldman edge detection algorithm for recognizing spiral or ring patterns in the disc. According to the manifold theory, the complexity of these patterns is related to the complexity of the `homoclinic lobes' formed by the invariant manifolds. The simulation was performed using a new N-body code based on a Cartesian grid solver of Poisson's equation using fast pre-conditioning techniques (Kyziropoulos et al. 2016, 2017). The invariant manifold theory is one of the main current theories for modeling spirals beyond the ends of bars (see Dobbs & Baba 2014). It has been developed in two versions: the `apocentric' manifolds (Voglis et al 2006) and the `flux tube manifolds' (Romero-Gomez et al. 2006, 2007), see Athanassoula (2012) and Efthymiopoulos (2010) for reviews and further references.
References:
- Athanassoula, E.: 2012, Mon. Not. Roy. Astron. Soc., 426, L46
- Dobbs, C. and Baba, J.: 2014, Pub. Astron. Soc. Australia, 31, 40.
- Efthymiopoulos, C., 2010: The European Physical Journal Special Topics, 186, 91
- Kyziropoulos, P., Efthymiopoulos, C., Gravannis, G., and
- Patsis, P.: 2016, Mon. Not. Roy. Astron. Soc., 463, 2210
- Kyziropoulos, P., Filelis-Papadopoulos, C.K., Gravvanis, G., and Efthymiopoulos, C.: 2017. `A parallel Self Mesh-Adaptive N-body method based on approximate inverses'. J. Supercomputing, Online first, DOI 10.1007/s11227-017-2078-7
- Kyziropoulos, P., Filelis-Papadopoulos, C.K., Gravvanis, G., and Efthymiopoulos, C.: 2017, `Toward the design of a novel hybrid parallel N-body method in scope of modern cloud architectures', J. Supercomputing, online first, DOI 10.1007/s11227-017-2140-5
- Patsis, P.: 2006, Mon. Not. Roy. Astron. Soc., 369, L56
- Romero-Gomez, M., Masdemont, J.J., Athanassoula, E. and Garcia-Gomez, C.: 2006, Astron. Astrophys., 453, 39
- Romero-Gomez, M., Athanassoula, E., Masdemont, J.J. and Garcia-Gomez, C.: 2007, Astron. Astrophys., 472, 63
- Voglis, N., Tsoutsis, P. and Efthymiopoulos, C.: 2006, Mon. Not. Roy. Astron. Soc., 373, 280
Numerical simulation of the axisymmetric ideal force-free pulsar magnetosphere
Numerical simulation of the axisymmetric ideal force-free pulsar magnetosphere with Aristotelian dissipation in the current sheet (lines with arrows: poloidal magnetic field; color scale: poloidal electric current density; distances in units of the light cylinder radius). Only the equatorial current sheet survives beyond the light cylinder, as expected in Contopoulos, Kalapotharakos & Kazanas 2014, and seen very clearly in Cerutti, Philippov, Parfrey & Spitkovsky 2015 (adapted from Contopoulos 2016, "Are there two types of pulsars?", Monthly Notices, 463, L94).
Sticky Orbits and Boxy Structures in Galaxies
A significant role for the morphology of 3D bars play the chaotic orbits that are found to be sticky to the rotational tori (Vrahatis et al. 1997) around the stable periodic orbits belonging to the families x1v1 and x1v1' (Skokos et al. 2002). These families are introduced in the system at the vertical 2:1 resonance and are considered as the backbone of the boxy/peanut (b/p) bulges observed in edge-on disk galaxies. The sticky chaotic orbits support simultaneously the b/p morphology in edge-on views and boxy features in face-on views. The figure at the top (a) summarizes the contribution of all significant orbits in a 3D Ferrers bar model that participate in enhancing b/p bilges at a characteristic energy (Patsis & Katsanikas 2014a). It gives the (z,pz) projection of the 4D phase space of x1 orbits perturbed in the pz direction, at Ej=-0.41. We indicate with black and grey "*" symbols the location of the x1v1 and x1v1' periodic orbits respectively. Red and green "x" symbols indicate the two branches of x1v2 (Skokos et al. 2002). The "▲" at (z,pz=(0.1,0.42) marks the location of the orbits of the x1mul2 family that also contribute to the reinforcement of a b/p morphology of the galactic bulge.
A characteristic examples of a sticky chaotic orbit that support simultaneously boxy edge-on and face-on morphologies are given in (b).
These sticky chaotic orbits exist in a certain range of energies. The face-on views of two more peanut-supporting orbits are given in (c) and (d) (Patsis & Katsanikas 2014b).
References:
Patsis P.A., Katsanikas M., 2014a, MNRAS 445, 3525 (arxiv)
Patsis P.A., Katsanikas M., 2014b, MNRAS 445, 3546 (arxiv)
Skokos Ch., Patsis P.A., Athanassoula E., 2002, MNRAS 333, 847
Vrahatis M., Isliker H., Bountis T.C., 1997, IJBC 7, 2707
For a detailed study of the phase space in 3D rotating Hamiltonian systems see:
Katsanikas M., Patsis P.A., Contopoulos G., 2013, IJBC 23, 1330005
Katsanikas M., Patsis P.A., Contopoulos G., 2011, IJBC 21, 2321
Katsanikas M., Patsis P.A., 2011, IJBC 21, 467
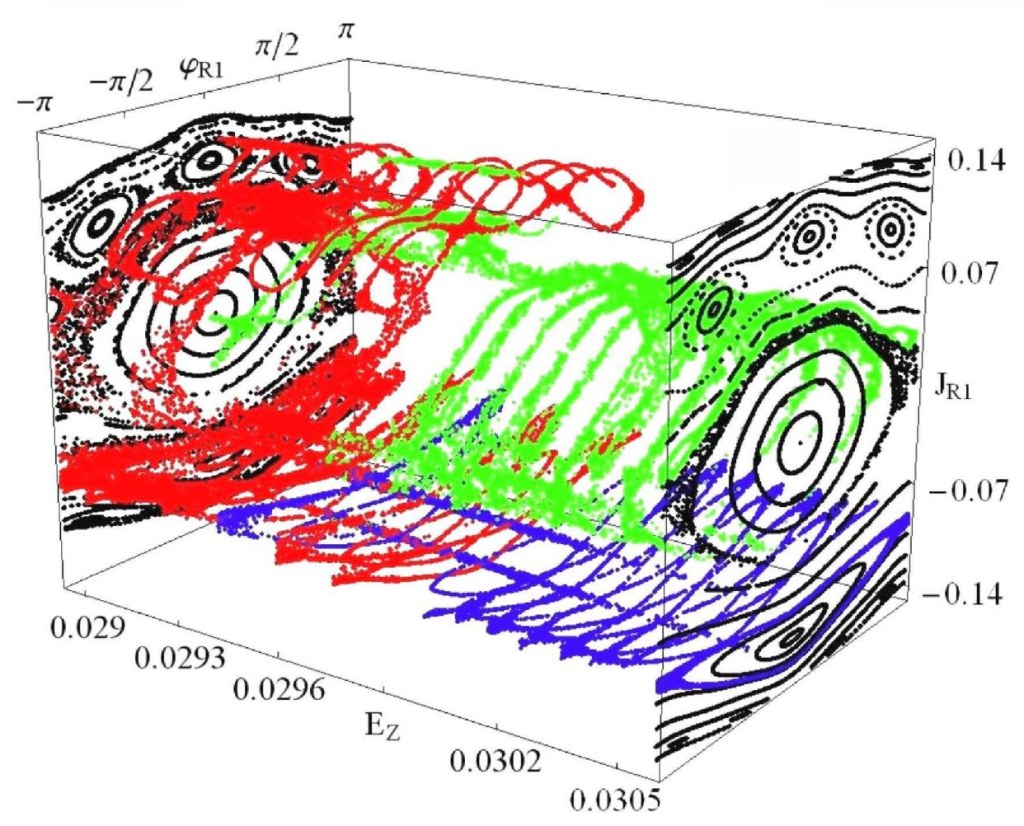
The Speed of Arnold Diffusion
The phenomenon of Arnold diffusion is important in a number of applications in solar system dynamics and plasma physics. The above figure, published in Efthymiopoulos and Harsoula, Physica D, 2013 (in press), shows a visualization of Arnold diffusion in a set of variables arising after a so-called optimal normal form construction using a special computer-algebraic program. According to theory, at a crossing domain of multiple resonances, the normal form construction allows to express the equations of motion as a Hamiltonian system of two degrees of freedom. This is perturbed, however, by a third degree of freedom appearing in the so-called `remainder' of the normal form. After a very slow drift in this third dimension (corresponding, in the figure, to the long edge of the framed parallelepiped), the orbits by-pass the barriers (invariant tori) of the 2D dynamics, and thus transit from one resonance to another. The timescale for this phenomenon is millions, or billions of characteristic periods of the orbits (see Efthymiopoulos and Harsoula 2013 for details).
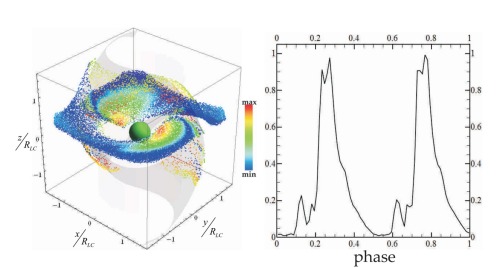
Trajectories of Particles in 3D Dissipative Pulsar Magnetospheres
We calculate realistic trajectories of particles in 3D dissipative pulsar magnetospheres and compute their Lorentz factor under the influence of both the accelerating electric field E? and curvature radiation-reaction. We determine the radiation intensity as a function of pulsar phase and thus generate realistic γ-ray light curves. Left-hand panel: the distribution of intensity as observed by an observer situated 75o from the rotation axis of an orthogonal rotator. Right-hand panel: associated γ?ray light-curve. Notice that the emission region is closely associated with the magnetospheric current sheet (after Kalapotharakos, Harding, Kazanas & Contopoulos 2012).
Structures supported by Chaotic Orbits
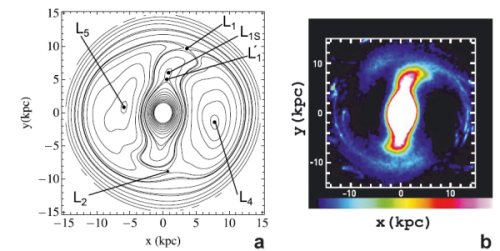
Models based on orbital theory indicate that the observed structures in disk galaxies (bars and spirals) can be supported by particles in chaotic motion. Here is an example of a model based on a potential estimated from near-infrared observations of the barred-spiral galaxy NGC 1300 (Kalapotharakos et al. 2010, 403, 83).
(a) The effective potential isocontours of the model. We have one stable (L1S) and five unstable (L4, L5, L1, L1', L2) Lagrangian points indicated with arrows. (b) The colour-scaled density response of a stellar disk after imposing this gravitational field. We observe the appearance of a typical grand design barred spiral morphology. The spirals, and to a large extent the "ansae" type bar are supported by particles in chaotic motion. A typical orbit supporting this structure during a time corresponding to ten bar rotation can be seen here (Patsis, Kalapotharakos, Grosbol 2010, MNRAS 408, 22; Patsis 2012, AApTr 27, 113).
Confined tori near a Hamiltonian Hopf bifurcation
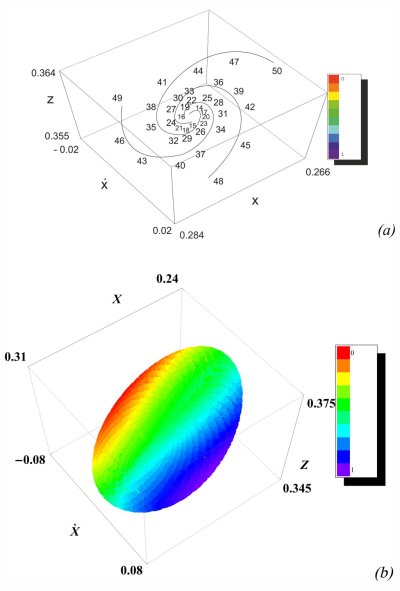
We have studied the orbital behavior in the neighborhood of complex unstable periodic orbits in a rotating 3D autonomous Hamiltonian system of galactic type. At a transition of a family of periodic orbits from stability to complex instability (also known as Hamiltonian Hopf Bifurcation) the four eigenvalues of the stable periodic orbits move out of the unit circle. Then the periodic orbits become complex unstable. In a recent paper (Katsanikas, Patsis, Contopoulos 2011, to appear in the International Journal of Bifurcation and Chaos) we first integrated initial conditions close to the ones of a complex unstable periodic orbit, which is close to the transition point. Then, we have plotted the consequents of the corresponding orbit in a 4D surface of section. To visualize this surface of section we used the method of color and rotation (Patsis and Zachilas 1994). We found that the consequents are contained in nearly 2D "confined tori". Then, we investigated the structure of the phase space in the neighborhood of complex unstable periodic orbits, which are further away from the transition point. In these cases we observed clouds of points in the 4D surfaces of section. The transition between the two types of orbital behavior is rather abrupt.
March 2011
Example processing and analysis performed on NOAA active region (AR) 9077, observed by the Michelson Doppler Imager (MDI) magnetograph onboard the Solar and Heliospheric Observatory (SoHO). This is the AR that gave the famous “Bastille day flare” on 2000 July 14th. (Right) A white‐light image of the solar disk with the AR bounded by a box (notice the complex of dark sunspots comprising it). (Lower left) The AR in white light, observed nearly simultaneously by the Transition Region and Coronal Explorer (TRACE) extreme ultraviolet (EUV) imager, with the inferred velocity flow field (curves). (Middle left) A patch of the SoHO/MDI photospheric magnetogram containing the AR. The gray curves on top indicate the results of the three‐dimensional magnetic-field extrapolation we applied to the magnetogram. (Upper left) To assess the quality of the extrapolation, we have plotted EUV TRACE observations on top of the same magnetogram. Notice the qualitative agreement between extrapolation results and actual observations (from a successful Marie Curie Actions proposal entitled "Solar Magnetic Eruptions: Understanding and Forecasting (SoME-UFo)" by M. K. Georgoulis, 2010).
January 2011
Nonlinear force-free numerical reconstruction of the global coronal magnetic field corresponding to the photospheric radial field of the so-called `Halloween 2003’ period (Carrington rotation 2009). Field-line color according to the twist parameter \alpha=curlB/B (I. Contopoulos, C. Kalapotharakos, M. Georgoulis 2011, Solar Physics).
November 2010
The picture of this month is from the recent succesful presentation of the PhD Thesis of P. Tsoutsis.
In this thesis, the connection between the theory of invariant manifolds emanating from unstable periodic orbits, and the generation of non-axisymmetric structures in strongly nonlinear models of barrred-spiral galaxies is studied. We first apply the theory of invariant manifolds in the case of the family of unstable short period orbits around the unstable points L1, L2 of a rotating N-body system. We find a direct link between the so called `bundles of preferential directions' of the invariant manifolds (plotted in configuration space) and the density maxima of the bodies of the simulation which produce spiral arms beyond corotation.
A chain of stars, with initial conditions along the invariant manifolds, defines a flow which can be shown to maintain the apocenters of the chaotic orbits correlated for long time intervals. This correlation can be described analytically by a soliton-like solution of an equation giving the positions of the apocenters of the chaotic orbits (Voglis 2003). We further elucidate this mechanism by demonstrating that the invariant manifolds are responsible for stickiness effects, which result in a significant slowing down of the rate of chaotic escapes in an otherwise non-compact region of the phase space. Extending the theory of invariant manifolds to other families of unstable periodic orbits we find a new phenomenon called `coalescence' of the invariant manifolds. Namely, the superposition of all the unstable invariant manifolds of many different unstable periodic orbits (for the same value of the Jacobi constant), enhances the density along the bundles of preferential directions.
This phenomenon becomes efficient precisely in the area where the invariant manifolds are found to support the spiral density maxima of the N-body particles. The above picture shows the coalescence of the invariant manifolds of 7 different unstable periodic orbits (namely the -1:1, -1:1 of multiplicity 2, -2:1, PL1, -4:1, 4:1, 3:1) for the same value of the Jacobi constant.
October 2010
Regions of various escape times of chaotic orbits, having initial conditions in a small area near an island of stability (gray color in the right of the figure) in the case of the “standard map”. Red color corresponds to fast escapes (after 1-5 iterations), yellow to slower escapes (after 5-10 iterations), green to even slower escapes (10-100 iterations) and blue to the slowest escapes (after more than 100 iterations). The limits between the various regions of different escape rates coincide with the stable asymptotic curves (black curves) of the unstable periodic orbits lying in this region (see for details and explanation the reference: “Stickiness in Chaos”, G. Contopoulos and M. Harsoula, 2008, Int. J. Bif. Chaos, 18, p.2929).